搜索结果: 1-15 共查到“Volterra”相关记录95条 . 查询时间(0.062 秒)
基于Lotka-Volterra 的城市客运走廊机动化交通方式竞争模型
客运走廊 出行群体 交通方式 竞争模型
2018/2/6
为了优化城市交通结构、缓解城市交通拥堵问题,本文在考虑城市客运走廊内 3 种不同类型的居民出行群体的基础上,以Lotka-Volterra 模型为基础建立了公共交通与私人交通的宏观竞争模型.并分析了不同交通方式的竞争强度及不同群体出行规模对模型的稳定性与演化结果的影响.结果表明,交通方式的竞争强度和不同出行群体的规模比例是影响交通方式间竞争激烈程度与其竞争结果的重要因素.当竞争较为激烈时,最终只有...
Modeling causal structures:Volterra's struggle and Darwin's success
Modeling Causal inference Volterra Predator-prey-model Darwin Coral atolls
2016/6/15
The Lotka-Volterra predator-prey-model is a widely known example of model-based science. Here we reexamine Vito Volterra's and Umberto D'Ancona's original publications on the model, and in particular ...
Measuring Volterra kernels
Volterra nonlinear system the kernel linear pseudo noise electroacoustic transducer
2015/8/13
Volterra series have been in the engineering literature for some time now, and yet there have been few attempts to measure Volterra kernels. This paper discusses techniques for measuring the Volterra ...
In this paper we carefully study the analysis involved with Volterra series. We address system-theoretic issues ranging from bounds on the gain and incremental gain of Volterra series operators to the...
In this paper we discuss the question of when the Volterra series is appropriate for nonlinear circuits. We determine that the Volterra series representation is appropriate for circuits with fading me...
Fading memory and the problem of approximating nonlinear operators with Volterra series
Continuous nonlinear operator volterra series operator nonlinear dynamic system
2015/8/13
Using the notion of fading memory, very strong versions of two theorems are proved. The first is that any time-invariant (TI) continuous nonlinear operator can be approximated by a Volterra series ope...
针对非线性模拟电路软故障诊断的难题, 基于Volterra 核二次型分布—–Wigner Ville 分布(WVD), 提出一种故障特征提取的新方法. 首先计算待测试电路(CUT) 的Volterra 核; 然后对该Volterra 核进行WVD转换, 得到WVD函数, 从中提取出故障特征, 完成非线性模拟电路的软故障诊断. 仿真实验结果表明, 该方法能有效地解决
故障混叠难题, 提升故障元件检...
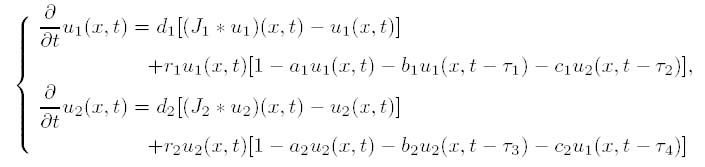
本文研究一类具有非局部扩散的时滞Lotka-Volterra竞争模型
行波解的存在性问题.通过利用交叉迭代技巧,我们可以把行波解的存在性转化为寻找一对适当的上下解,这篇文章中的结果推广了已有的一些结果.
卫星信道中基于部分解耦的volterra均衡算法
卫星信道 部分解耦 非线性 均衡
2013/5/31
对信道中大功率放大器产生的非线性特性实现快速有效地均衡是提高卫星通信系统性能关键技术之一。文中首先建立了基于volterra级数的卫星信道模型,并分析了信道对二维调制信号所产生的非线性影响;针对基于最小均方误差实现的volterra均衡器收敛速度慢这一问题,提出了基于复基带volterra模型的部分解耦均衡算法,该算法使均衡器线性权系数收敛于线性滤波器最优解,并用拉格朗日乘数法构造了新的代价函数,...
基于DFP的二阶Volterra模型及其对Rössler混沌序列的预测
二阶Volterra模型 Davidon-Fletcher-Powell算法 DFPSOVF Rö ssler混沌序列预测
2017/1/12
为克服最小二乘法或归一化最小二乘法在二阶Volterra建模时参数选择不当引起的问题,在最小二乘法基础上,应用一种基于后验误差假设的可变收敛因子技术,构建了一种基于Davidon-Fletcher-Powell算法的二阶Volterra模型(DFPSOVF).给出参数估计中自相关逆矩阵估计的递归更新公式,并对其正定性、有界性和τ(n)的作用进行了研究.将DFPSOVF模型应用于Rössl...
Multilevel Correction For Collocation Solutions of Volterra Integral Equations With Proportional Delays
delay integral equation geometric mesh collocation method superconvergence
2012/8/10
In this paper we propose a convergence acceleration method
for collocation solutions of the linear second-kind Volterra integral
equations with proportional delay qt (0 < q < 1). This convergence
a...
基于Volterra级数的自适应水声信号预测方法研究
声学 水声信号 Volterra自适应滤波器 多步预测
2015/4/10
背景噪声和混响干扰是声纳目标探测中的主要干扰源,如何有效地减小它们对声纳工作特性的影响一直是水声信号处理关注的焦点。利用Volterra 级数理论,建立水声信号的非线性动力学模型,通过对水声信号的局部预测,实现对背景噪声的降噪和混响干扰的抑制。结合二阶Volterra 自适应滤波器和基于奇异值分解的自适应滤波算法,分别采用直接法和迭代法完成了对水声信号的一步及多步预测。仿真结果表明,基于Volte...
Numerical Solution of the Fredholme-Volterra Integral Equation by the Sinc Function
Fredholme-Volterra Integral Equation Sinc Function Collocation Method
2013/1/30
In this paper, we use the Sinc Function to solve the Fredholme-Volterra Integral Equations. By using collocation method we estimate a solution for Fredholme-Volterra Integral Equations. Finally conver...
基于乘积耦合Volterra模型的短时交通流预测
交通工程 预测模型 Volterra级数 短时交通流 乘积耦合
2012/3/15
基于混沌序列固有的非线性和确定性机制以及Volterra级数的非线性表征能力,提出一种短时交通流预测的三阶Volterra模型。针对Volterra模型随阶数增加复杂度以幂次方增加的问题,研究了该模型的乘积耦合近似实现结构。首先,采用互信息法和虚假邻点法选取时间延迟和嵌入维数,并采用小数据量法计算Lyapunov指数判定交通流是否具有混沌特性;然后,建立三阶Volterra滤波器的乘积耦合近似实现...
张志涛研究员等在Bose-Einstein Condensates和Volterra-Lotka竞争系统研究中取得重要成果
张志涛研究员 Bose-Einstein Condensates Volterra-Lotka 竞争系统 研究 成果 极限
2012/2/23
自从物理学家提出用耦合Gross-Pitaevskii方程组来描述Bose-Einstein凝聚态以来,对这个奇异扰动的Schrodinger方程组及其极限中的phase separation现象出现了大量的研究, 许多国际著名数学家如现代变分理论创始人A. Ambrosetti以及E.N.Dancer,S.Terracini, T. Bartsch,Juncheng Wei等都有突出成果。


